О математике и пандемиях. Автор Ahiin
Часть 1.
Disclaimer 1.
Я НЕ ВРАЧ и не являюсь профильным специалистом-эпидемиологом, а свою последнюю научную работу на тему матмоделирования эпидемий написал без малого 20 лет назад. По всем вопросам здоровья, коронавирусов и смысла жизни консультируйтесь с лечащим врачом, не будьте «Чудаками».
Disclaimer 2.
Ниже будет некоторое количество графиков. Перед их построением я умышленно декалибровал и упростил модель, отстроившись от параметров COVID-19. Приведенные графики демонстрируют развитие эпидемии некоторого условного вируса в некоторой условной популяции в условном времени. Не делайте предсказаний о ходе текущей пандемии, опираясь на мои картинки, не будьте «Чудаками».
Ну, а теперь — поехали! По понятным причинам, нонче подскочил интерес ко всякому пандемическому и всевозможные математические и не очень математические модели бродят по соцсетям стаями. Число же эпидемиологов и специалистов по системам дифференциальных уравнений и вовсе превысило все мыслимые переделы. Тем не менее, во всем этом информационном буйстве странным образом обойдены молчанием перколяционные, они же стохастические имитационные, модели. Этот недостаток мы сейчас немедленно исправим. Кстати, впервые о подобных моделях (как и многом другом) я прочитал в замечательной книжке Гулда и Тобочника «Компьютерное моделирование в физике».
Устроена перколяционная модель обманчиво просто. Для начала мы создаем общую компьютерную модель индивидуума, участвующего в эпидемии. Что-нить не слишком сложное: здоров, болен, выздоровел, умер и условия перехода между состояниями. На основе статистических данных об исследуемой популяции, каждый конкретный экземпляр случайным образом наделяется теми или иными характеристиками, а ля возраст, пол (если это важно), крепость иммунитета и т.п. Наделав кучку таких конкретизированных экземпляров, мы размещаем их в вершинах некоторого графа, имитирующего социальные связи. После этого остается задать условия передачи инфекции между индивидуумами, заразить несколько первых счастливчиков и дать старт эпидемии.
Большим преимуществом подобного подхода является простота модификации и свобода от многочисленных априорных допущений, позволяющие быстро прогнать модель для самых разных, даже экзотических сценариев. Примеры мы увидим ниже. Обратной стороной данного метода является то, что строгое математическое описание и анализ возникающих в такой системе эффектов зачастую очень сложен (мягко говоря). Впрочем, поэкспериментировать это нам не помешает.
Довольно болтовни, к делу! Возьмем 16 миллионов пацаков и равномерно разместим на гиперсфере. Соседей соединим в граф каким-нибудь шаблоном. Это упрощение для социального графа, но мы, слава богу, не минздрав, чтоб заморачиваться. Заразу будем распространять каждый день двумя путями. Во-первых, пацак на каждом шаге может с некоторой вероятностью заразиться от больных соседей. Во-вторых, с некоторой другой вероятностью, он может на каждом шаге заразиться от случайного пацака, не входящего в его окружение (эффект «общественного транспорта»). Ну и наконец, сама болезнь. Период бессимптомного носительства примем длиной 10 шагов, после чего пацак показывает симптомы и больше в распространении не участвует. Следующие 10 шагов он болеет, имея на каждом шаге некоторый шанс скопытиться. После этого он выздоравливает (если доживет, конечно). Начальный посев примем 100 пацаков.
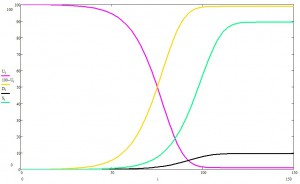
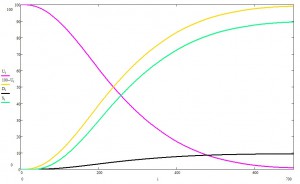
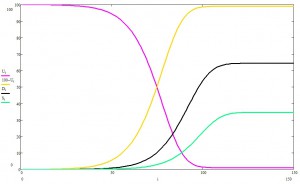
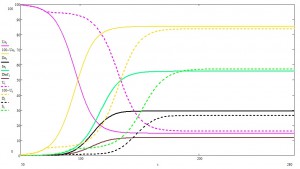
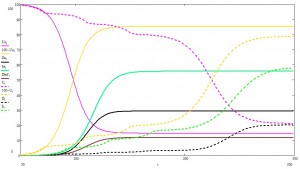
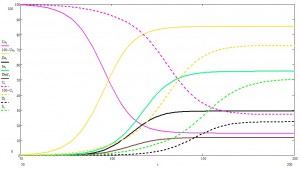
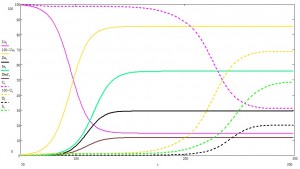
При указанных условиях, получаем следующую картинку:
Фиолетовым показан процент незараженных пацаков, желтым — заболевших, зеленым — выздоровевших, черным — сами понимаете.
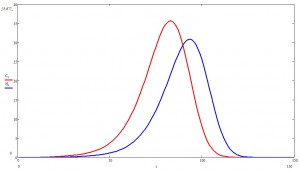
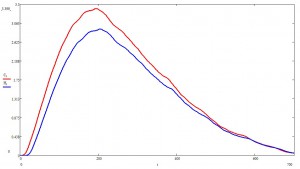
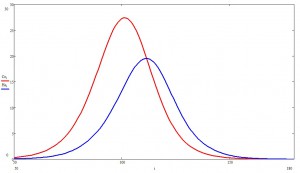
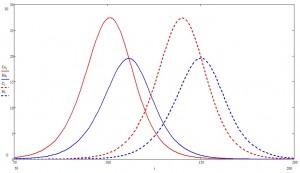
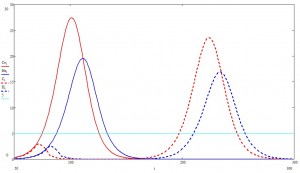
Посмотрим теперь на больных поближе:
Здесь на каждом шаге красненьким показан процент болеющих, но еще бессимптомных пацаков, а синим — проявляющих симптомы.
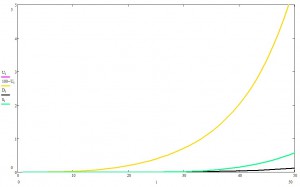
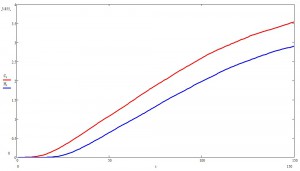
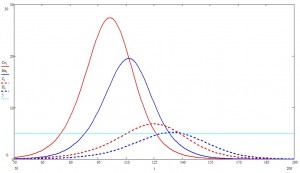
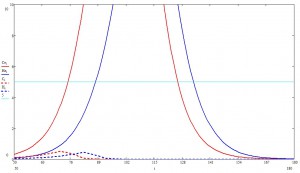
Теперь вернемся к первому графику и взглянем попристальней на начальную фазу эпидемии (легенда та же):
Да-да. Эта та самая экспонента, которой СМИ уже всю плешь проели. Если на пальцах, то происхождение этой самой экспоненты таково: в условиях, когда число носителей мало, а общественная жизнь поставляет носителю новых случайных незараженных пацаков, число новых заражений прямо пропорционально числу носителей. Математически это записывается в виде дифференциального уравнения
решением которого является, вы жеж не поверите, экспонента. Такая штука много где в природе встречается, в частности, одним из ярчайших примеров, во всех смыслах, является неуправляемая цепная реакция. Потом, с ростом числа носителей, хялява для инфекционного агента заканчивается, но в рамках текущей пандемии, например, эта фаза еще не пройдена.
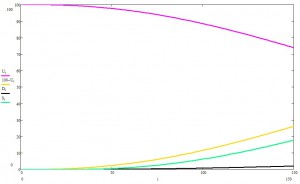
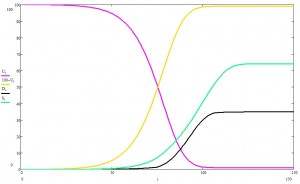
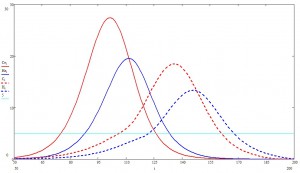
Давайте теперь примем меры, скажем, отправим пацаков на выходные и закроем общественный транспорт и мероприятия. В рамках модели, это будет означать, что инфекция распространяется теперь только вдоль ребер социального графа, от родственника родственнику, от друга к другу. Ну и да, очевидно, чатлане спохватились не сразу, поэтому меры примем, когда заболеет 1000 пацаков.В том же масштабе времени:
В прошлом эксперименте, эпидемия без «ограничительных мер» успела потухнуть, а здесь еще и даже до пика расти и расти.
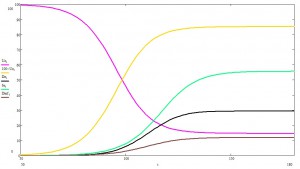
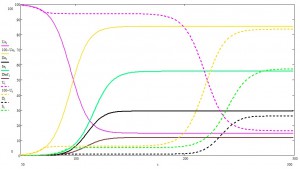
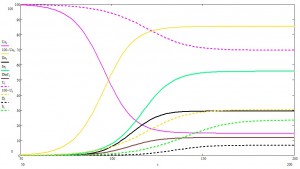
Взглянем на эпидемию целиком:
Как видите, время эпидемии растянулось в немалые разы.
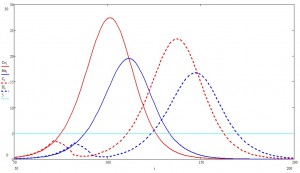
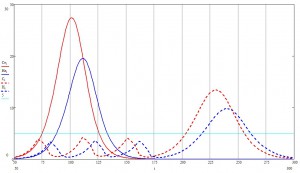
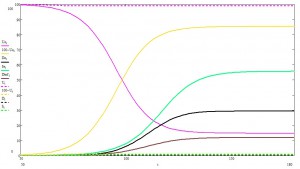
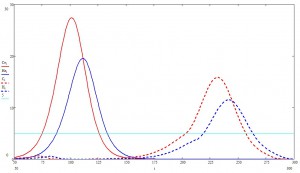
Особенно важен пошаговый график:
Принятые меры на порядок снизили количество одновременно болеющих. Почему это важно, будет видно ниже.
Возможно, на графиках не так хорошо заметно, но основной эффект в том, что после принятия мер экспоненциальный рост числа заболевших почти моментально сменяется степенным. Грубо на пальцах, это можно объяснить следующим образом: каждый новый заболевший становится сам источником заразы и начинает заражать всех вокруг (эдакий инфекционный принцип Гюйгенса). Но это «вокруг» ограниченно лишь немногочисленными незараженными соседями, которые заражаясь сами, передают инфекцию дальше. Таким образом, вокруг очага образуется «волновой фронт», который с некоторой постоянной скоростью расползается во все стороны (кто сказал «эйконал» —тот молодец), а число инфицированных —это объем «пространства», заметенный волновым фронтом, который (чистая геометрия) пропорционален некоторой степени пройденной фронтом дистанции.
Ну и последний эксперимент на сегодня. Будем щедры к системе здравоохранения, но при этом добавим реализму. Пусть порог ее насыщения — одномоментно болеющие 10% популяции (это заведомо гораздо круче реальности) и пусть вероятность склеить ласты у пацака, которому не досталось койки, возрастает в 10 раз. Пусть, наконец, чатлане не озаботились каникулами для пацаков (обсчитывать такой сценарий для случая с каникулами смысла нет, у минздрава в самый пиковый момент останется тройной запас прочности). Тогда получим:
Точка насыщения достигается в районе 75 шага, как раз над буковкой i. Чтоб вы вдруг не подумали, что «минздрав не нужен», вот вам графики для случая, когда он не то, чтобы перенасытился, а его не было изначально (добро пожаловать в средневековье):
Такие дела. Не болейте!
Часть 2.
Disclaimer 1
Я математик, а не врач. По всем вопросам здоровья, коронавирусов и смысла жизни консультируйтесь с медиками, не будьте глупыми людьми.
Disclaimer 2
По этическим соображениям, результаты работы модели, калиброванной по параметрам COVID-19, публиковаться не будут. Возможно, вы с моим решением не согласны, но вам придется с этим жить.
Как мы увидели в прошлой части, режим самоизоляции достаточно эффективен, в частности он сбивает экспоненциальный рост числа заболевших до степенного и тем самым позволяет снизить нагрузку на здравоохранения до приемлемой (“flatten the curve”, ага). Тем не менее, режим самоизоляции длится очень долго, наносит огромный ущерб экономике и возникает резонный вопрос: нельзя ли обойтись пусть более жесткими, но краткосрочными мерами?
Для наглядности экспериментов я слегка модифицировал инфекционный агент, сделав его чуть менее заразным, для большей иллюстративности интересующих нас эффектов. Помимо этого, я снизил порог насыщения минздрава до 5% популяции (это все равно очень и очень много). И да, чтоб не слишком ранить чувствительные души, шанс смерти индивидуума, которому «не досталось койки», вырастает теперь в три раза, а не в десять, как раньше. Цените мой гуманизм! Остальные параметры такие же (самое важное: инкубационный период, когда пацак заразен, длится 10 дней и столько же длится период лечения).
Для указанных параметров, расчёт хода эпидемии в отсутствии каких-либо ограничительных мер выглядит так:
Легенда так же: фиолетовым показан процент незараженных пацаков, желтым — заболевших, зеленым — выздоровевших, черным — скончавшихся. Дополнительно, коричневая кривая показывает количество смертей в идеальном случае неограниченных ресурсов здравоохранения (мы к ней будем стремиться).
Пошаговый расклад выглядит так:
Здесь на каждом шаге красненьким показан процент заболевших, но еще бессимптомных пацаков, а синим — проявляющих симптомы.
Обе эти картинки далее будут использоваться нами в качестве референса, для оценки эффективности принимаемых мер.
Рассмотрим теперь меры, которые будут применяться. Состояние, когда не только минимизированы случайные контакты (выключен «общественный транспорт»), но и приняты меры по кратному снижению интенсивности продвижения заразы по социальным связям (чего мы ранее не рассматривали), будем условно называть «карантином», закавыченым, обратите внимание. Термин «карантин без кавычек» не только медицинский, но и юридический, и довольно суровый, поэтому «не нужен». Параметры заразности подобраны таким образом, чтобы в условиях «карантина» инфекция медленно и печально сдыхала за несколько сотен шагов, добирая несколько процентов популяции в процессе.
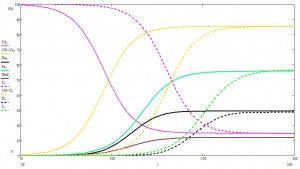
Итак, для начала попробуем ввести «наивный карантин». Запрем всех и вся на 15 шагов (логично ведь, инкубационный период и еще половинка на всякий случай). Более того, у ответственных чатлан ушки на макушке, меры введены уже на 20 шаге эпидемии (инфицировано 0.012% популяции). Что может пойти не так? Все.
Пунктирной линией показаны результаты «принятия мер».
Этот кажущийся парадоксальным результат вполне закономерен. «Карантинные» меры значительно сокращают количество циркулирующего в популяции возбудителя, но увы, недостаточно. После отмены ограничений вновь начинается экспоненциальный рост и эпидемия, практически в неизменном виде, просто оказывается несколько отложенной (напомню, что наша «задача минимум» — удержать синий график под голубенькой линией, предотвращая перегрузку системы здравоохранения).
Интересно, что если единственным средством в нашем распоряжении является такой 15-шаговый «наивный карантин», то применить его эффективнее на более поздних стадиях. Сравните, например, вариантом, когда мы его введем на 70 шаге:
Ситуация улучшилась, но не радикально. Замах-то был на рубль. Может мы зря пожадничали на срок «карантина»? Давайте сразу в три раза увеличим, чтоб наверняка. Даешь «карантин» на 45 дней!
Что ты будешь делать, а?!
Еще попытка? Давайте попробуем тактику «пунктирного карантина», вводя его трижды, на 70, 110 и 150 шаге (те же 15 шагов «карантина»):
И тут мы уже видим некоторый просвет. Уровень смертности для случая минздрава бесконечной мощности еще не достигнут, но ясно, что, продолжив резать нашего удава по частям, цели можно добиться, при этом, действительно сократив длительность эпидемии (экономическая целесообразность подобного тяни-толкая — это другой вопрос).
Можно ли качественно улучшить этот результат? Спешу обрадовать: да, причем значительно. Но для этого нам придется ввести в рассмотрение дополнительный фактор.
До сих пор в наших построениях руководящие структуры чатлан вели себя достаточно пассивно. В меру своих сил они организовывали лечение, уговаривали пацаков сидеть дома и, возможно, эцилоп бил немножко особо нерадивых по ночам. Да, так бывает и в реальности, но обычно меры по борьбе с эпидемией включают в себя поиск и изоляцию контактов заболевшего. Деятельность эта крайне трудоемкая, но и эффект от нее трудно переоценить. Действительно, давайте теперь всех соседей заболевшего по социальному графу отправлять в карантин. После этого он не сможет никого заражать, если уже инфицирован, и не сможет заразиться сам, если был здоров. При таких условия мы получим следующий ход эпидемии (мероприятия по изоляции начинаются на 20 шаге):
О! Как говорится, чтож вы раньше молчали? Слава тяжкому труду эцилопов, «карантин не нужен»! Пиковая нагрузка на здравоохранение в пределах допустимого, работать ему в таком режиме нужно сравнительно недолго, а кривая смертности провалилась даже ниже нашей целевой, коричневой. Счастье всем, и никто не уйдет обиженным!
К сожалению, эта картинка слишком хороша, чтобы быть правдой. Ресурсы спецслужб тоже исчерпаемы, в не меньшей мере, чем медицинские. Дабы не плодить дополнительные линии на графиках, пусть насыщение спецслужб происходит при все тех же 5% симптоматических (это такой же гипероптимизм как и с медиками, можете прикинуть сами, какой объём популяции придется на этом этапе контролировать):
Мда, все уже не столь радужно. Тут важно отметить следующее. Ход эпидемии гораздо чувствительнее к перегрузке спецслужб, нежели к перегрузке здравоохранения. Непродолжительная перегрузка здравоохранения приведет к некоторому росту отправивщихся в верхнюю тундру, это печально. Но даже незначительная перегрузка служб изоляции и контроля (обратите внимание на предыдущую пару графиков, синяя штриховая кривая самую малость превышает критический порог, даже не на полшишечки) ведет существенно более тяжелому характеру эпидемии, кратно увеличивая итоговое число погибших (я уж молчу про остальные неласковые последствия).
Важнейший вывод из изложенного выше: критически важно не допустить перегрузки служб, занимающихся отслеживанием и изоляцией контактных пацаков. Давайте снова попробуем ввести «наивный карантин» и посмотрим, что из этого получится (старт на 70 шаге, длиной 30 шагов, чтоб уж не ограничиваться полумерами):
Вот это покарантинили, вот это изолировались! Эпидемия сдохла!!!
Произошло следующее: благодаря «карантинным» мерам, зашивающиеся эцилопы получили передышку и сумели нагнать убегающий вперёд фронт эпидемии, а нагнав— выдали всем контактным по эциху с гвоздями и тем блокировали дальнейшее распространение инфекции. Слава товарищу майору! Кроме шуток.
Автор картинки Вася Ложкин (если вы вдруг не знали).
Забегая вперед, отмечу, что именно этот сценарий реализовался в Китае и нескольких других странах, которые меньше на слуху. Судя по действиям российского руководства, отрабатывается именно такой вариант.
Сразу возникает вопрос: может мы зря так размахнулись, давайте «карантин» на 15 шагов сделаем?
Да, но нет. Не надо жадничать!
Я уже не буду мучать притомившихся дополнительными графиками, отмечу лишь, что чем раньше начать принимать меры, тем короче будет «карантин». В рамках описываемой модели, на 50 шаге достаточно запереться на 25 шагов, на 30 шаге достаточно и 20. А, скажем, на 120 шаге хоть обкарантинься, контроль за распространением инфекции будет уже потерян.
Резюмируя: вовремя введенные «карантинные» меры в сочетании с активной работой специальных служб позволяют не только «сгладить кривую», но и полностью остановить развитие эпидемии. Ярким историческим примером является ликвидация вспышки натуральной оспы в СССР в 1960 году, ставшая возможной благодаря уникальной совместной операции КГБ, МВД и Минздрава СССР.
Такие дела. Не болейте!
Если вам понравился пост, вы можете оставить комментарий или подписаться на RSS и получать каждый новый пост из этого блога.

 English
English  Русский
Русский
Комментарии
Еще никто не комментировал.
Оставьте комментарий